PeleLMeX Verification & Validations
This section is work-in-progress.
Laminar Poiseuille flow
The laminar pipe flow or Poiseuille flow, is a basic test case for wall bounded flows. In the present configuration, the geometry consist of a circular channel of radius \(R\) = 1 cm aligned with the \(x\)-direction, where no-slip boundary conditions are imposed on EB surface. The flow is periodic in the \(x\)-direction and a background pressure gradient \(dp /dx\) is used to drive the flow.
The exact solution at steady state is:
where \(G = -dp/dx\), and \(\mu\) is the dynamic viscosity.
The test case can be found in Exec/RegTests/EB_PipeFlow, where
the input parameters are very similar to the PeleC counterpart of
this case.
The steady-state \(x\)-velocity profiles accross the pipe diameter at increasing resolution are plotted along with the theorerical profile:
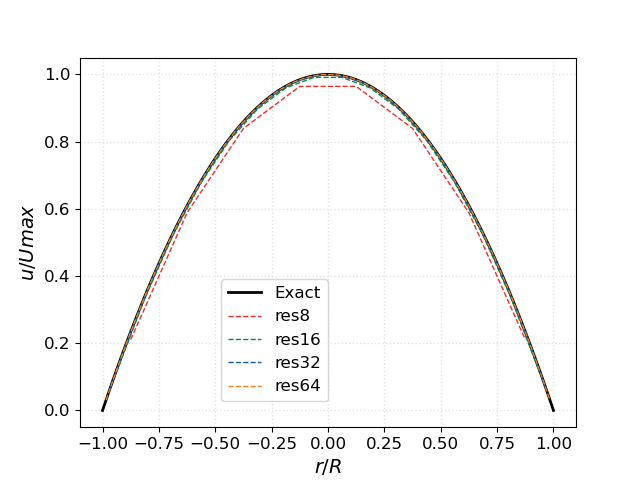
A more quantitative evaluation of PeleLMeX results is obtained by calculating the L2 norm of the error against the analytical profile:

showing second-order convergence for this diffusion dominated flow.
Taylor-Green vortex breakdown
The Taylor-Green vortex breakdown case is a classical CFD test case described in here <https://www1.grc.nasa.gov/research-and-engineering/hiocfd/> (case C3.3).
Building and running
The test case can be found in Exec/RegTests/TaylorGreen.
$ make -j 16 DIM=3 USE_MPI=TRUE TPL
$ make -j 16 DIM=3 USE_MPI=TRUE
$ mpiexec -n 16 $EXECUTABLE inputs_3d amr.ncell=64 64 64
The user can run a convergence study by varying amr.ncell.
Results
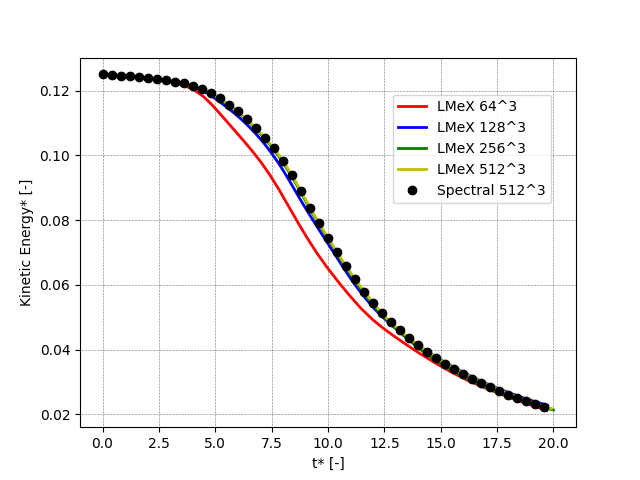
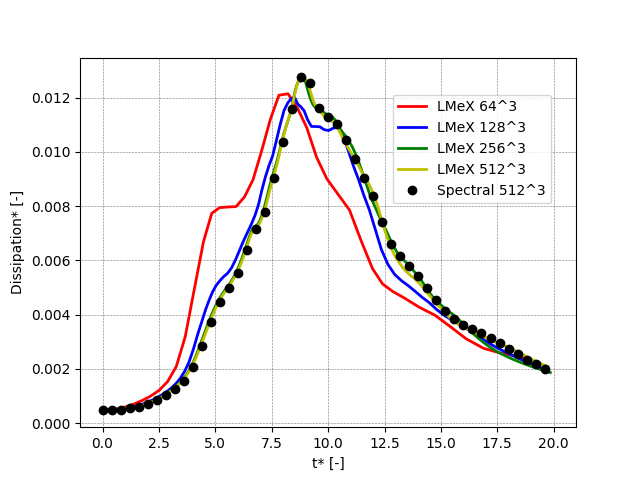
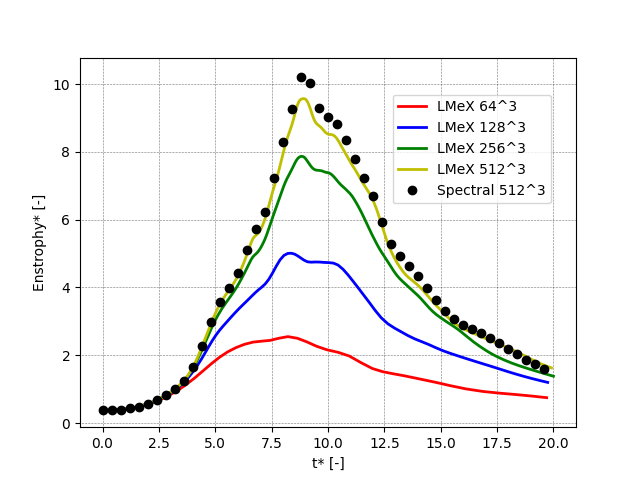
The following figures shows the kinetic energy, the dissipation rate and the enstrophy as function of time (all quantities are non-dimensional) for increasing resolutions (ranging from 64^3 to 512^3) and compared to the results of a high-order spectral solver with a 512^3 resolution.